Random Vector Functional Link Neural Network

Abstract

This paper includes process of Random Vector Functional Link Network, Tested on 10 of the UCI datasets, using k-fold cross validation method for tuning the hyper-parameter. Find the best parameter list for the algorithm. We also used one-hot encoding for multi-class classification.

Keywords: RVFL, One-hot Encoding, K-fold Cross Validation

*All codes are available at: https://github.com/LeslieWongCV/EE6222

Setup on which the code was tested

- python==3.7
- numpy==1.19.2

I. Random Vector Functional Link Network

A. Network

Random Vector Functional Link Network1 is a one layer Feedforward Neural Network, the weights and the bias of the RVFL is randomly generated and because RVFL is a Feedforward Neural Network, weights and bias are fixed during training. The structure of the RVFL is shown below as Figure.1

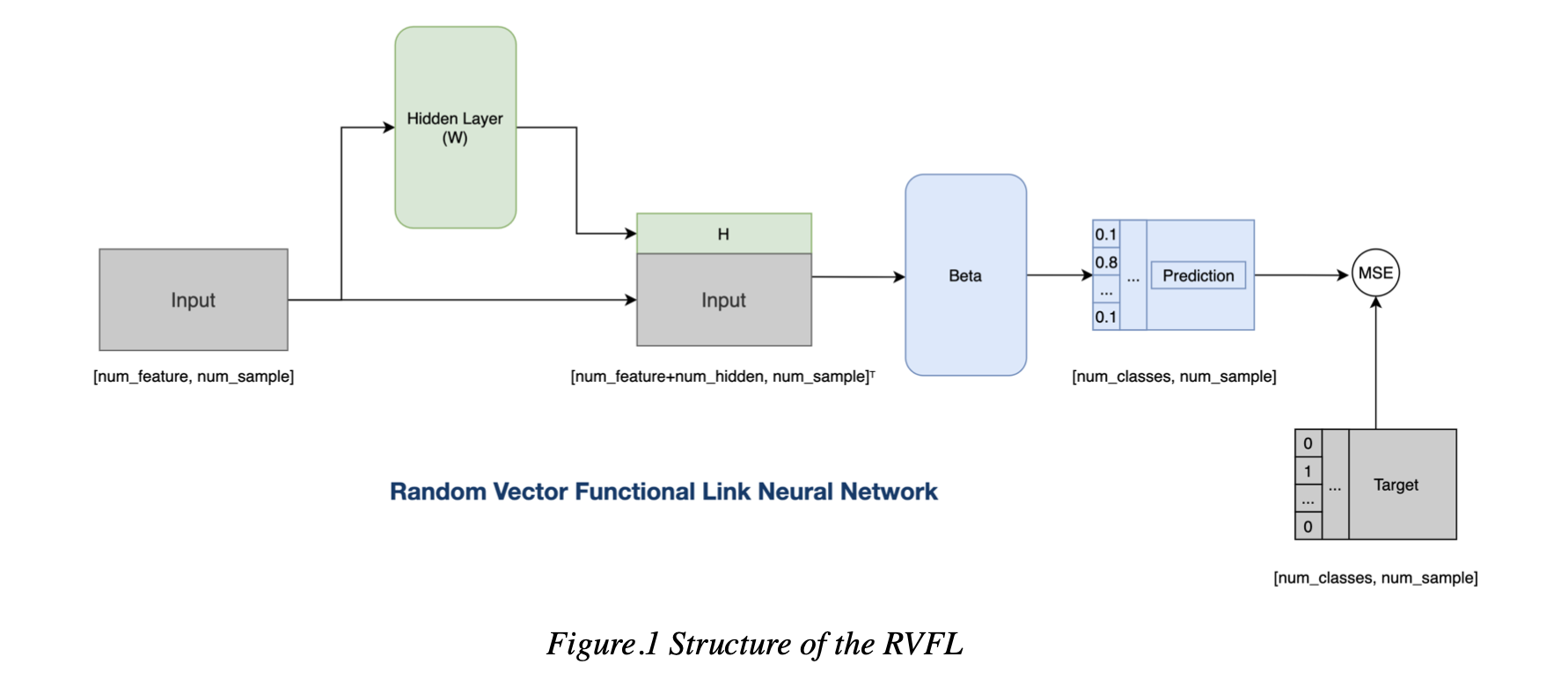
The output from the Activation Function is denoted as H(X), then H(X) is concatenated with the original data X, form the D. D = [H, X]. The output of the network is calculated by dot product of D and β. The neural node in the Figure.1 represents the set of all the neural nodes in a RVFL.

B. One-Hot Encoding

In this assignment, the dataset contains several Muti-classification case. Using 0 and 1 for output encoding could not solve the problem.
The One-Hot Encoding maps the features to the Euclidean space, which is more effective. For distance measuring in Regression, Classification and Clustering algorithms is of great importance. It solved the problem that the classifier cannot handle the attribute data and it also played a role in expanding features.

C. K-Fold Cross Validation

In this paper, we use k-fold cross validation for tuning the hyper-parameter list. In this method:

Repeat k times:

Step 1. Divide the dataset into k equal parts.  
Step 2. Take one copy each time as the validation set without repeating, use the other k-1 copies as the training set to train the model, and then calculate the accuracy of the model on the validation set.  
Step 3. Calculate the average accuracy for k times.   

For one set of the hyper-parameter, following the steps above can get the average accuracy. Change the hyper-parameter and repeat until find the best parameter list.

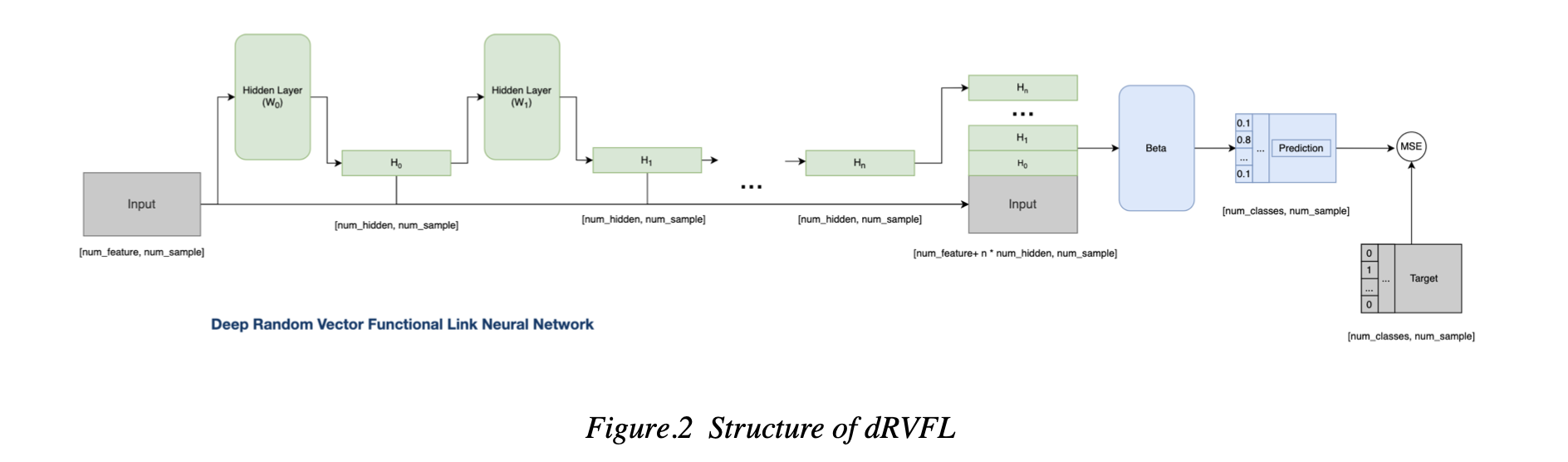
II. Deep Random Vector Functional Link Network

Deep Random Vector Functional(dRVFL) is an extended version of the RVFL, it has multiple layers.
Structure shown in Figure.2:

III. Experiments

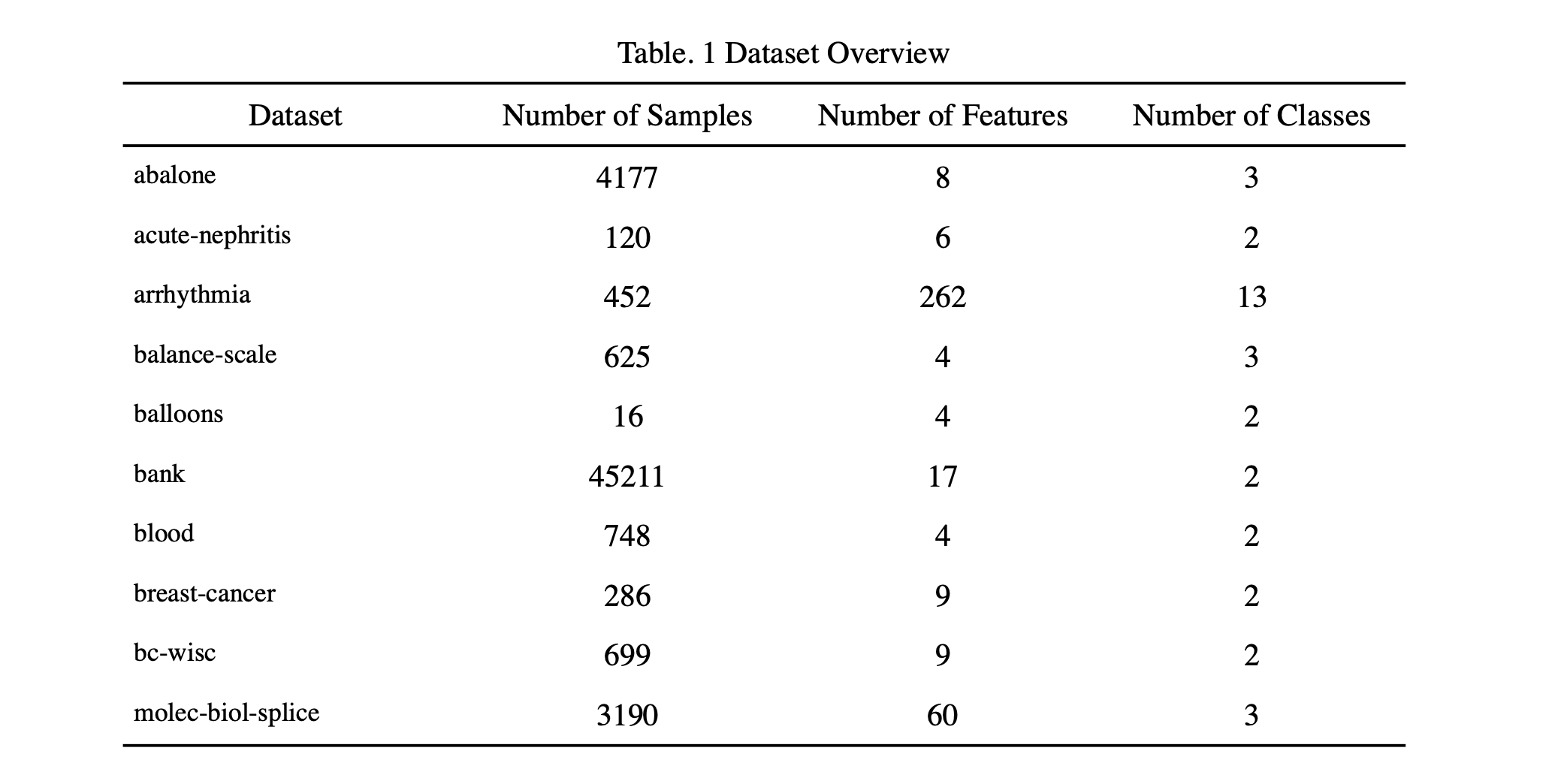
In this section, we evaluate the performances of RVFL on the 10 of UCI open-source datasets. The overview of the datasets using for training are show in Table. 1.

A. Validation and Testing of RVFL

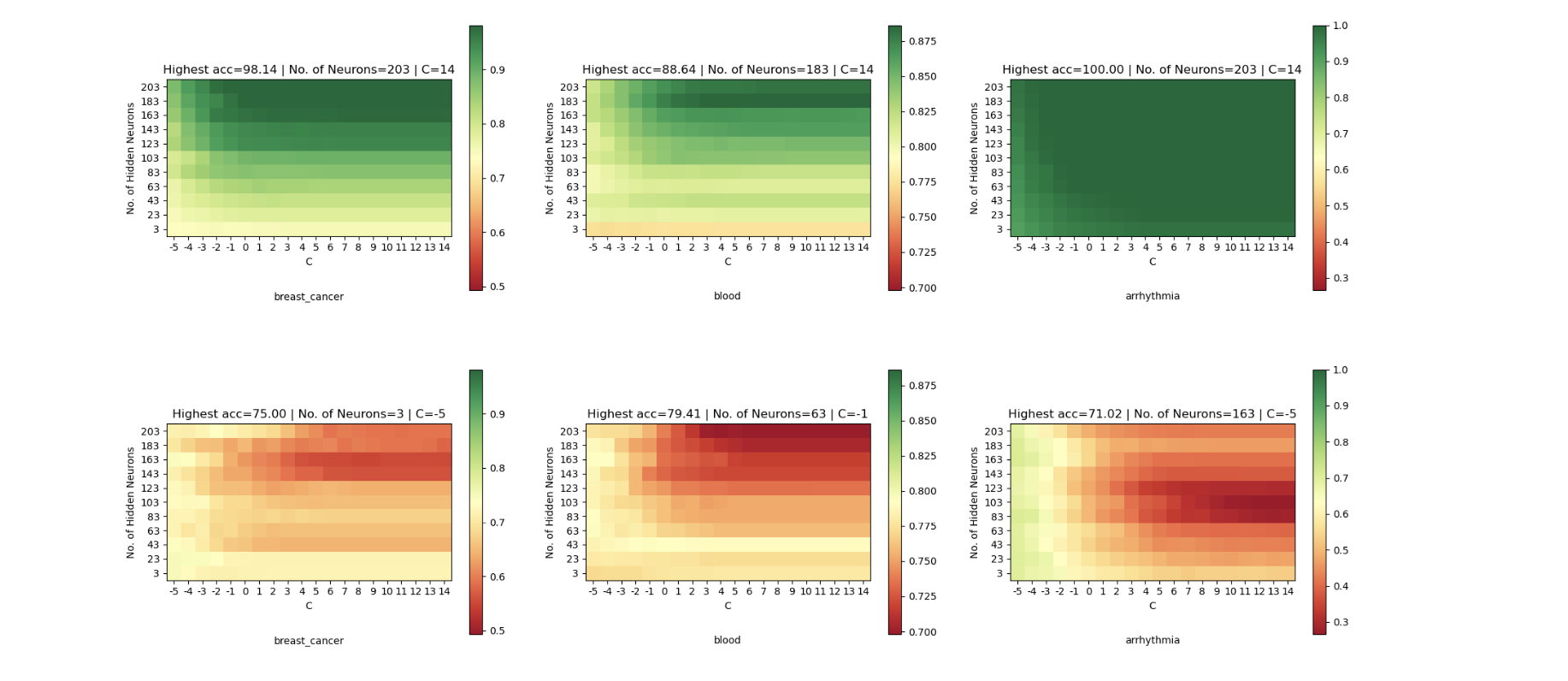
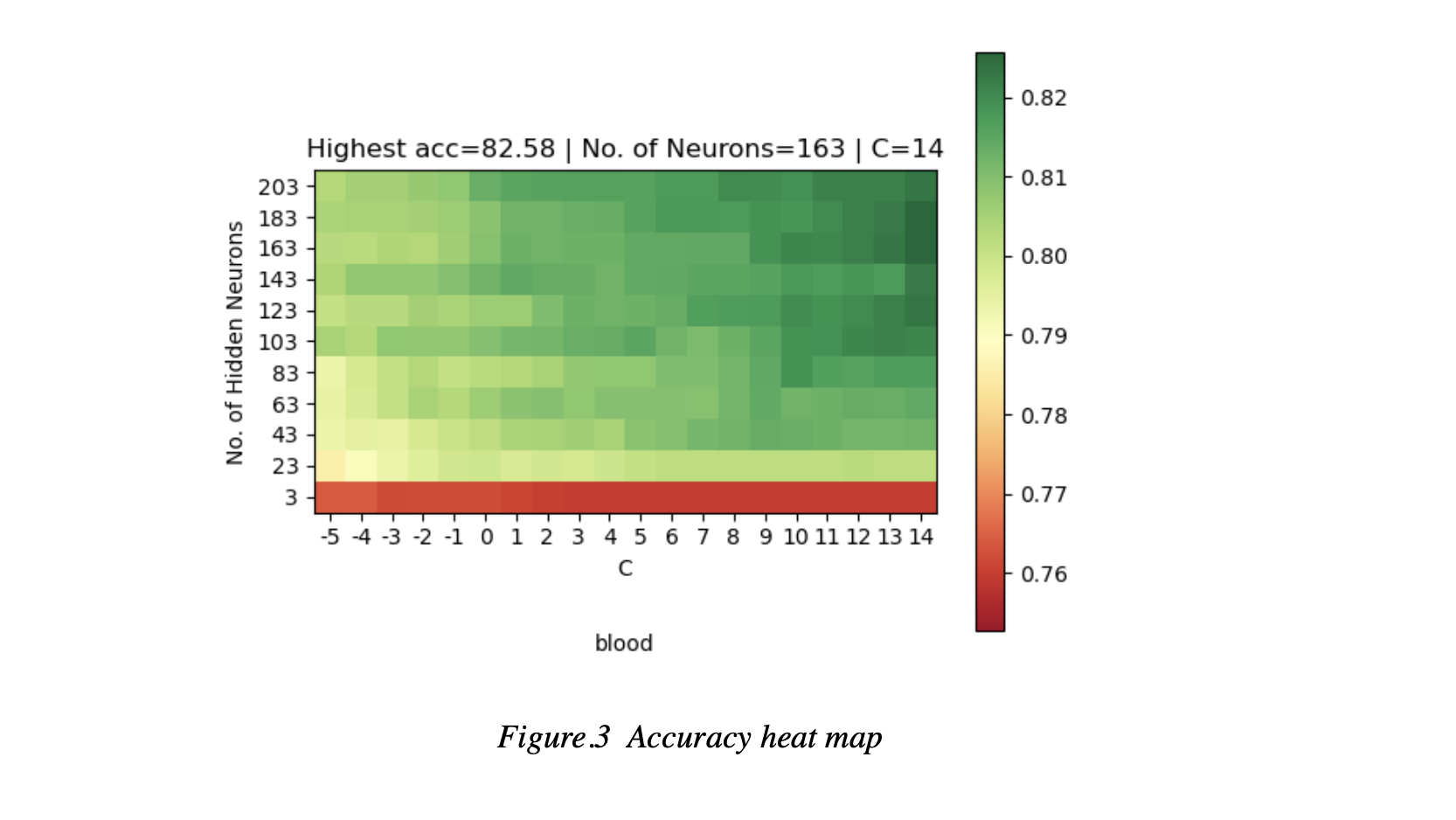
In each network we also compared the performance with different no. of neural and intensity of Regularization(C). Network with a bigger C means weaker in Regularization.We visualize the accuracy on different values of these parameters.

Direct Link

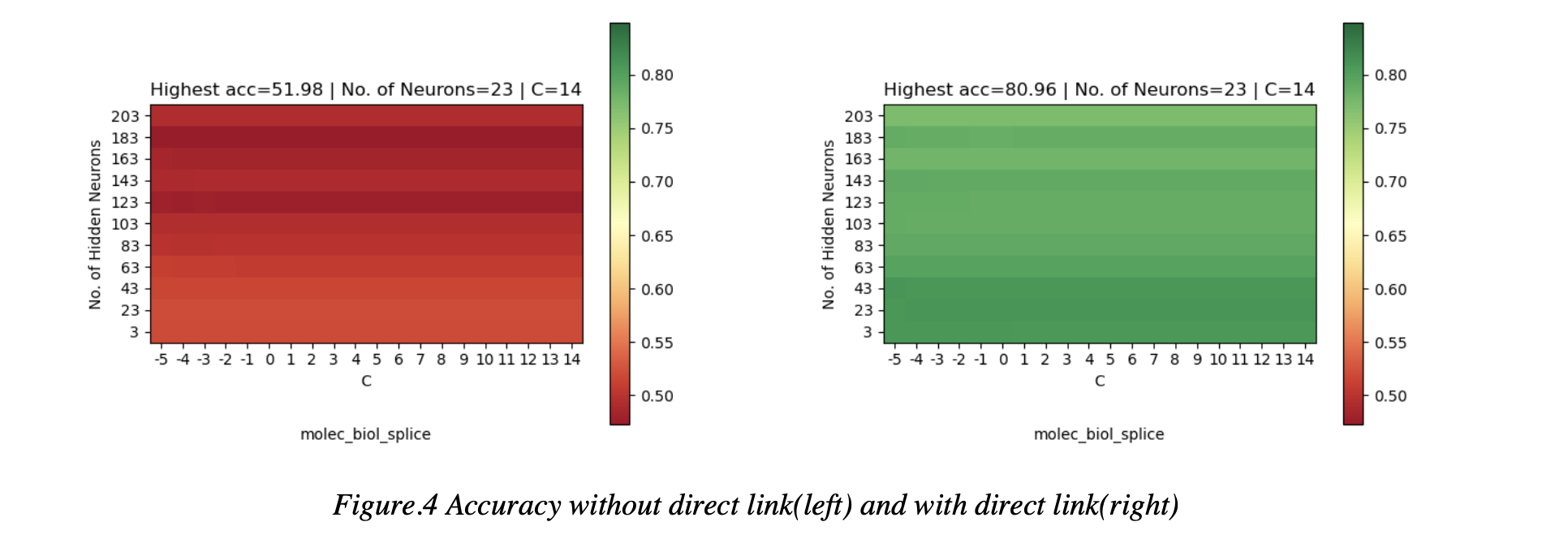
In the experiment we first conduct the research of the effect of the direct link from the input layer to the output. We found that when we drop the direct link in RVFL, the network becomes Multilayer Perception(MLP). The Results are shown at Figure.4. We visualize the accuracy on each dataset for RVFL with direct link(left) and RVFL without direct link(right).

Activate Function

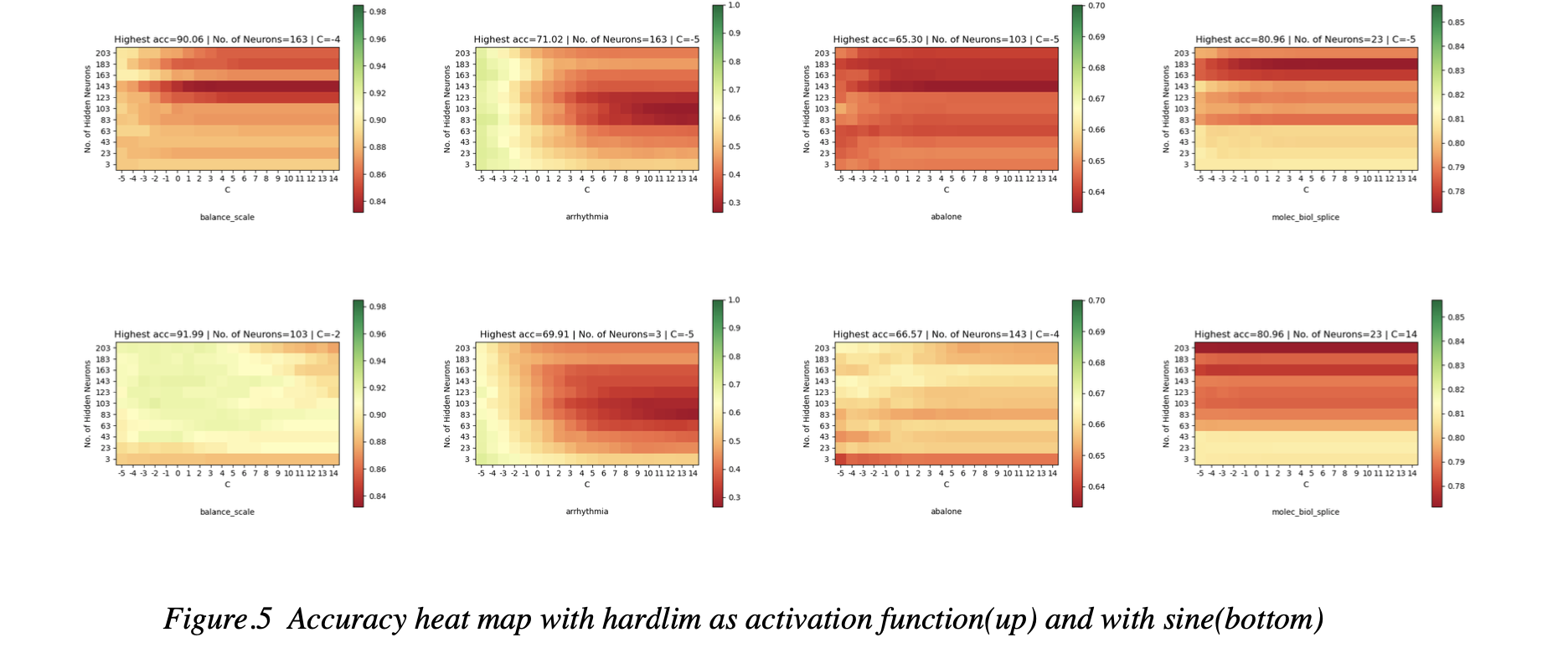
We then did the experiment with two activation functions: 1. sine, 2. hardlim on 10 datasets. Figure.5 shows the result of 4 datasets.

Regularization

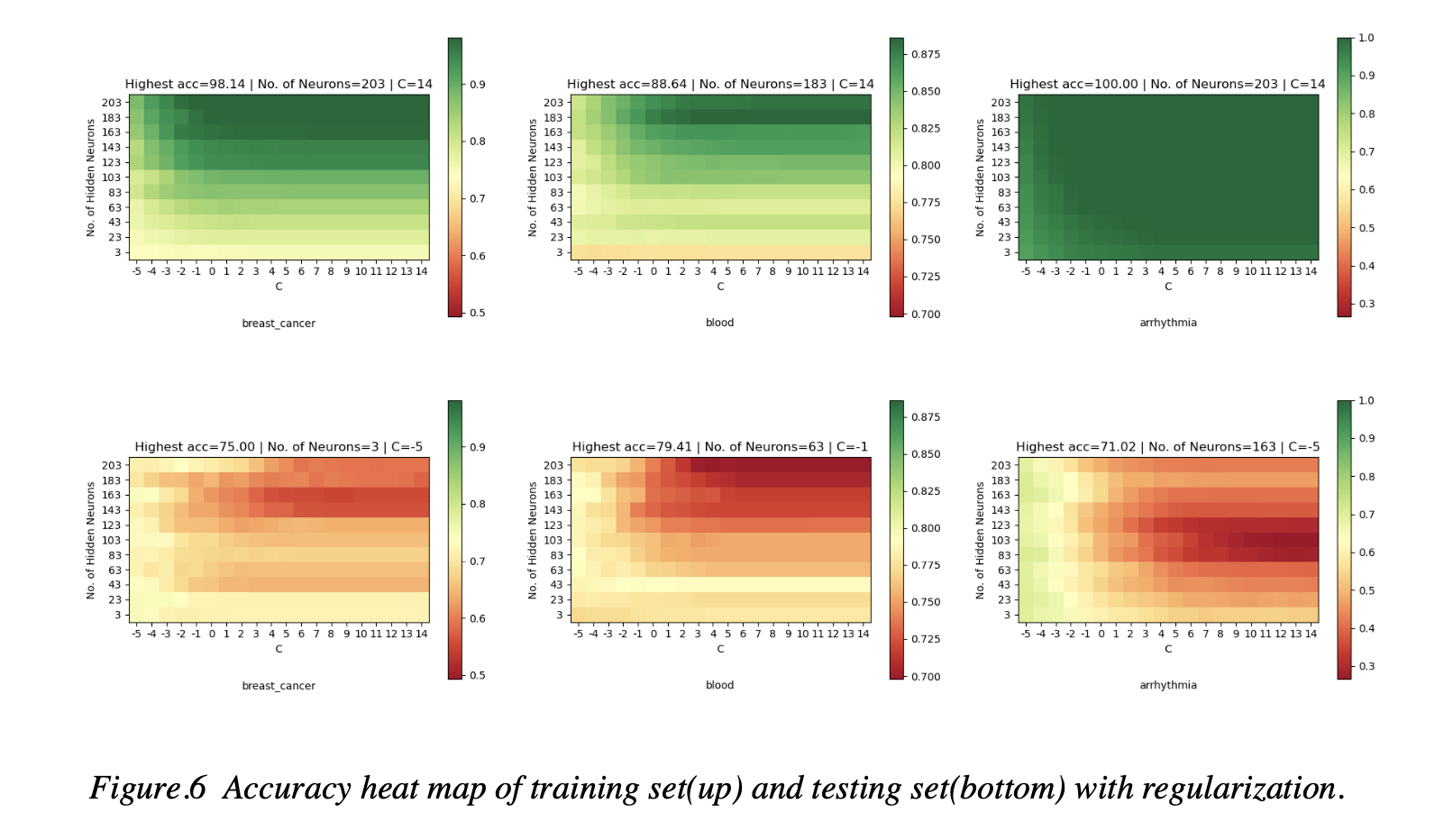
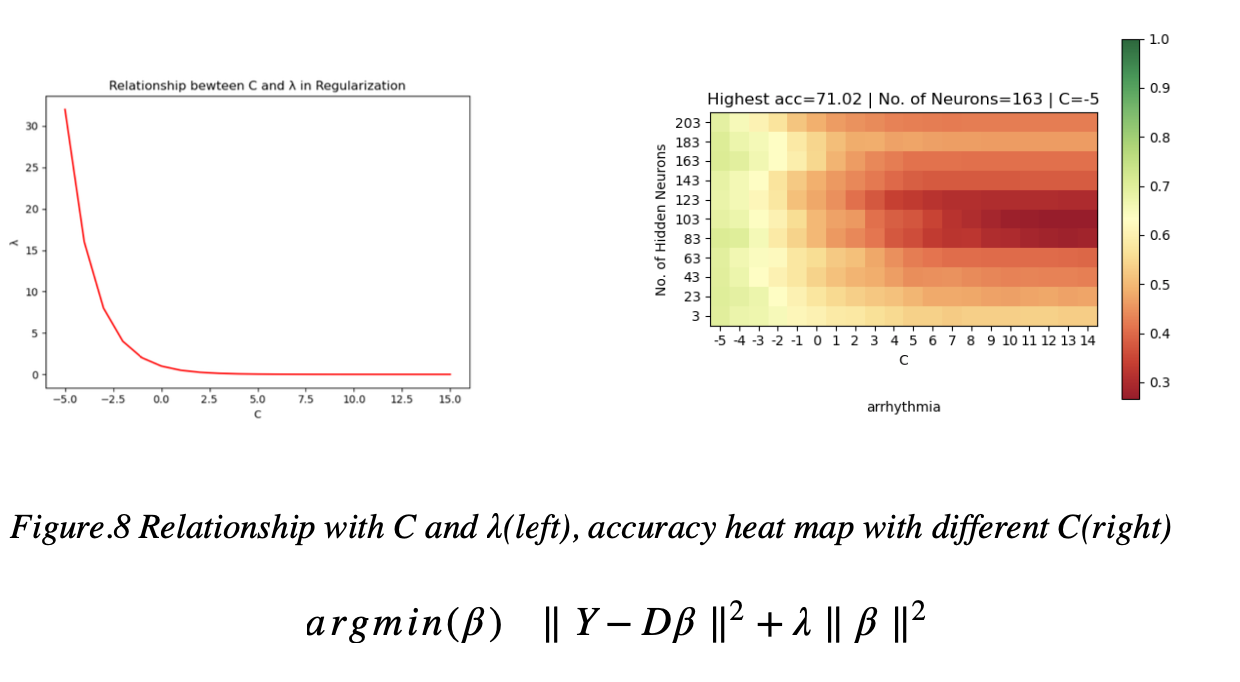
Last we find out that Regularization plays an important role in training. For model with more hidden neurons, if the Regularization is not strong, there would be an obvious overfitting. As shown in the Figure. For example, The upper right corner means complex model with almost no Regularization. Then the accuracy in training period and testing period is significant different.

While for those models with strong Regularization(left side in each graph), even if the model is complex, the testing accuracy is stable compared with weak Regularization, which means that overfitting problem is not significant when model has Regularization.

B. Validation and Testing of dRVFL

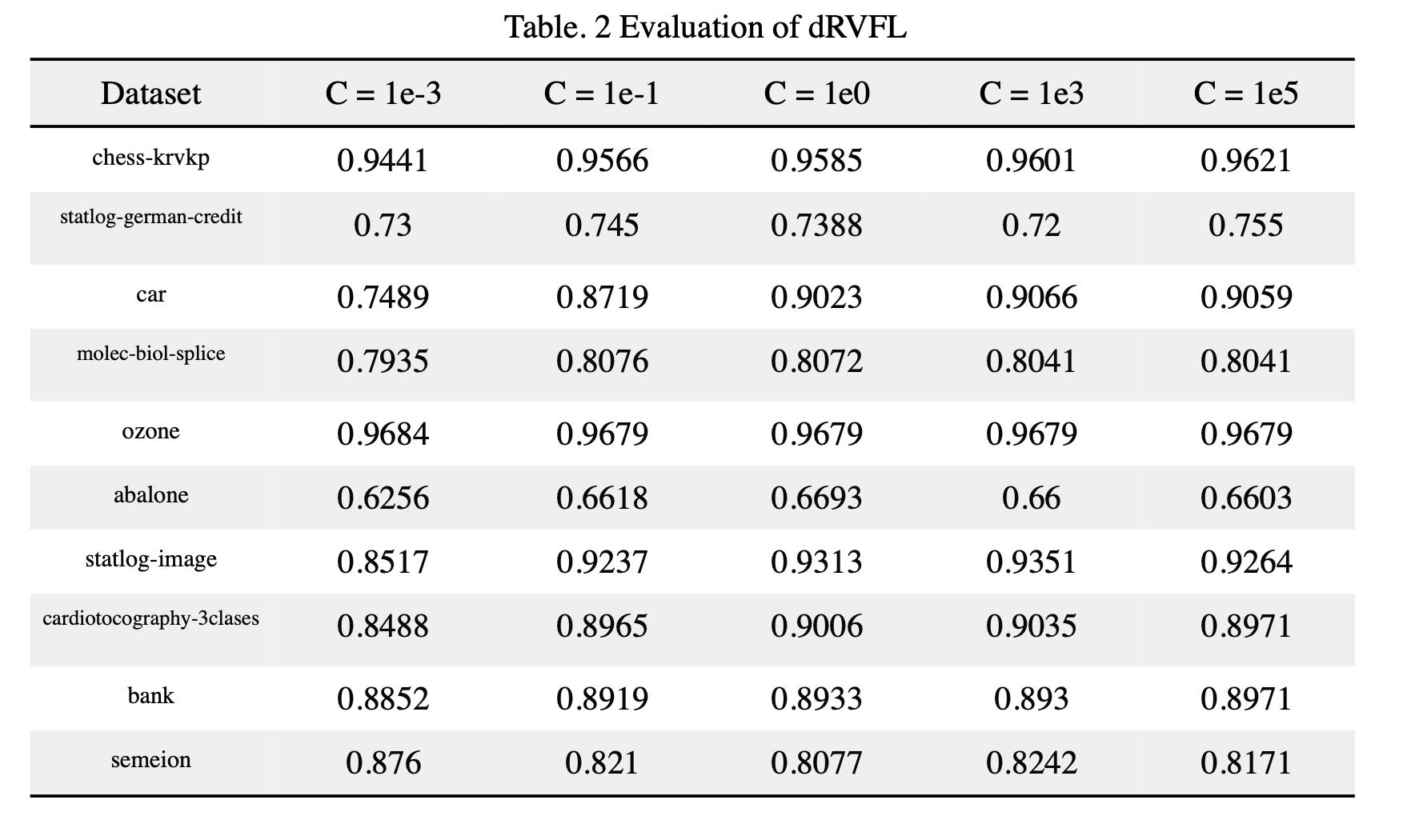
We also evaluate the dRVFL on following 10 datasets, and the results are shown below:

We tuned the nodes of each layer of the dRVFL, shown in Figure.7:

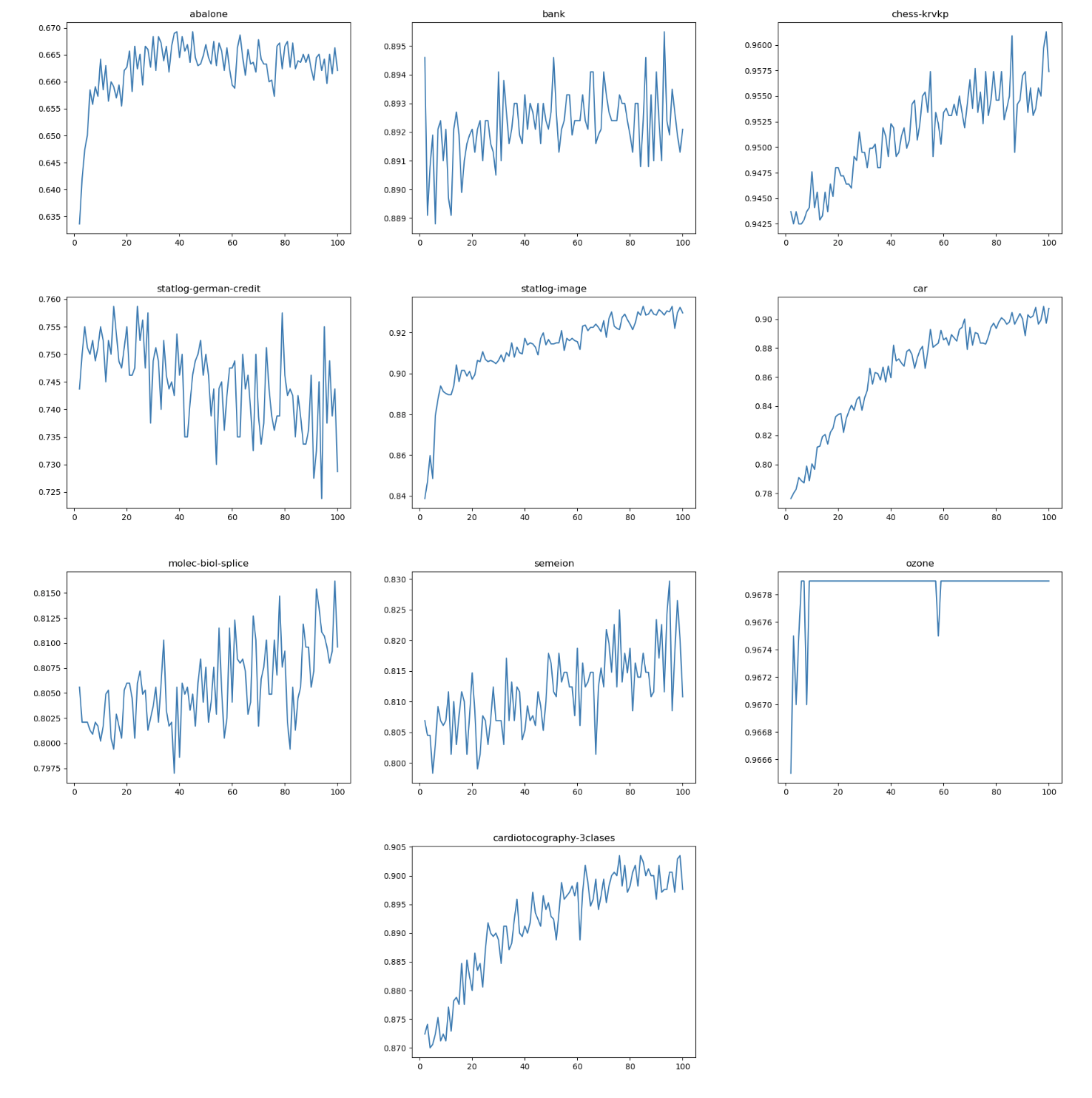
dRFVL with different no. of nodes.

III. Conclusion

In this paper, we discussed the basic concepts of RVFL and dRVFL The classification performance of two models is evaluated on 10 UCI datasets. Experimental results prove the effectiveness of these algorithms in solving classification problems in the real world.
We found that adding more layers would improve the accuracy, but in this dataset which contains limited samples, network that is too deep would not be helpful because of overfitting. We found in dRVFL, the number of nodes for each layer is of great significant.

A. Effect of Direct Links

We found that direct links improves the performance of the network, which is shown in Figure.4, and this is because of the direct link between the input and the output could be considered as a regularization for the hidden layer, because there is randomization in the hidden layer, so if we only use hidden layers, the network would not like to be stable and fit for the data input.

B. Performance comparisons of activation function

We found that in Ridge Regression based methods, the performance of sine is better than hardlim. And for Moore-Penrose pseudo inverse, sine is also better than hardlim in most cases.(Figure.5)

C. Performance of Moore-Penrose pseudo inverse and Ridge Regression.

In most datasets, the performance of Ridge Regression is better than pseudo inverse. And λ is equal to 1/2^C. We consider model as Ridge Regression when C in [-5, 0] and [1, 15] as Moore-Penrose as shown in Figure.8. We can observe that model with smaller C has better performance, and it is not likely to overfitting.

IV. References

[1] Husmeier, Dirk. “Random vector functional link (RVFL) networks.” Neural Networks for Conditional Probability Estimation. Springer, London, 1999. 87-97.
[2] Katuwal, Rakesh, Ponnuthurai N. Suganthan, and M. Tanveer. “Random vector functional linkneural network based ensemble deep learning.” arXiv preprint arXiv:1907.00350 (2019).
[3] Huang, Guang-Bin, Qin-Yu Zhu, and Chee-Kheong Siew. “Extreme learning machine: theory and applications.” Neurocomputing 70.1-3 (2006): 489-501.

Issues

The above is the description of all the work for the RVFL. If you encounter unclear or controversial issues, feel free to contact Leslie Wong.