Expectation Maximization and VAE

Expectation Maximization

EM is an iterative algorithm with latent variables.

We often find the parameters of the model using the sample that we observed, and use the maximum log likelihood function to get the parameter value. However, in some cases, the observed data we get has unobserved latent variable. Implicit data and model parameters (including latent variable), so it is impossible to directly maximize the log-likelihood function to obtain the parameters of the model distribution.

EM could solve the problem.

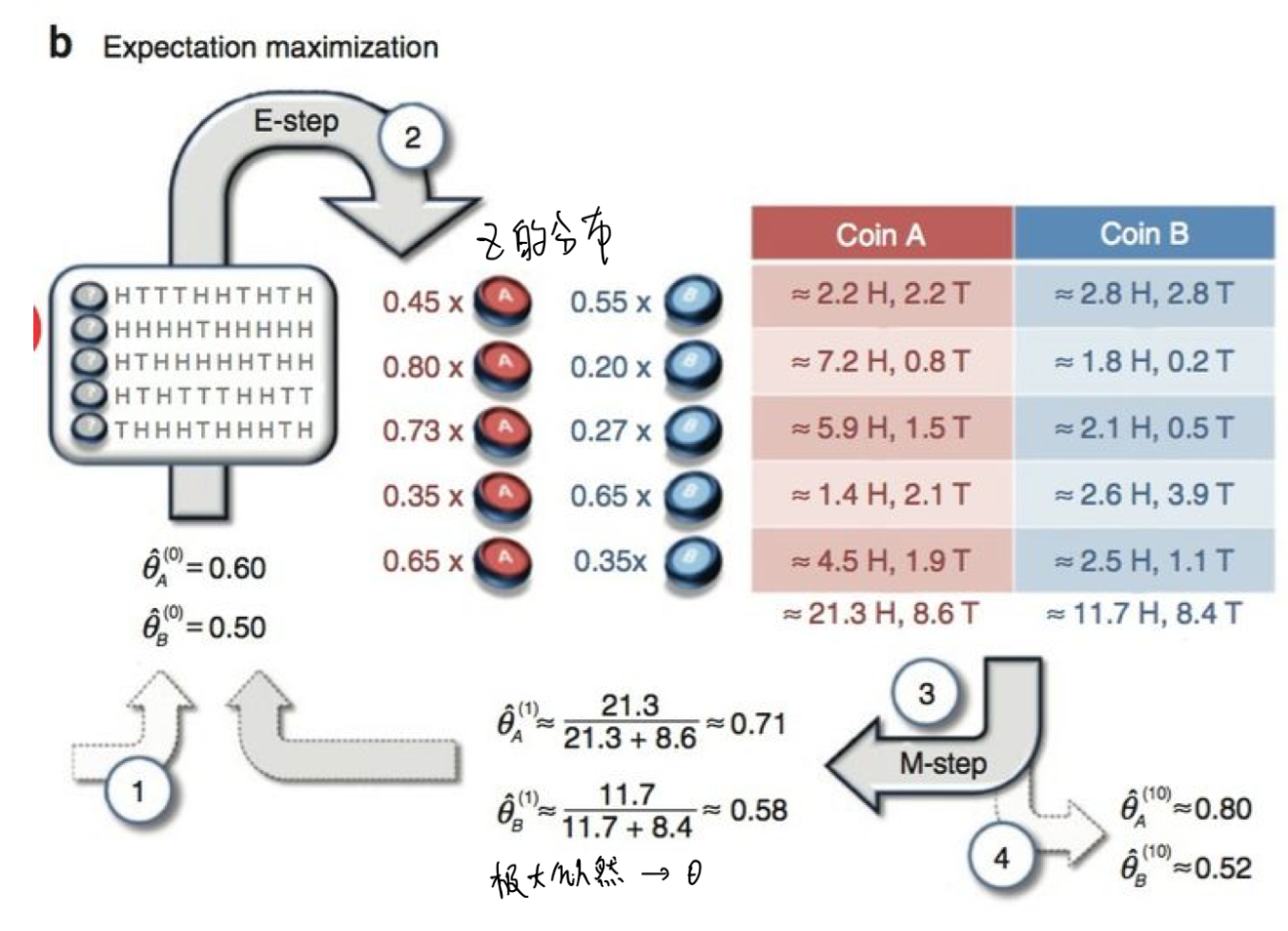
the Procedure of EM.

Variational Auto-encoders (VAE)

Introduction

VAE is an unsupervised generation algorithm. We all know Auto-encoder: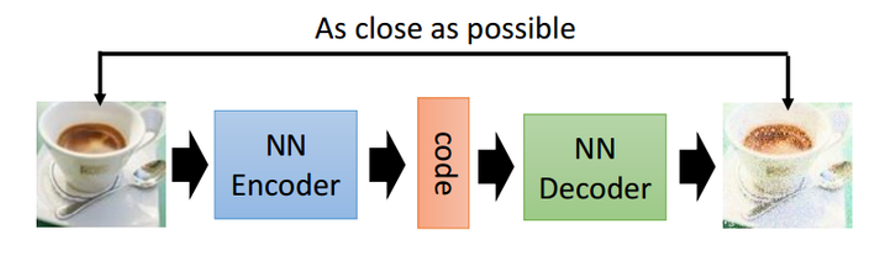

Structure of Auto-encoder.

But in this way, we can’t actually generate pictures arbitrarily, because we have no way to construct the latent vector by ourselves. We need to input and encode a picture to know what the hidden vector is. VAE can solve this problem.

VAE add restrictions in the encoding process, forcing the implicit vector generated by it to roughly follow a standard normal distribution. This is the biggest difference between it and the general auto-encoder.

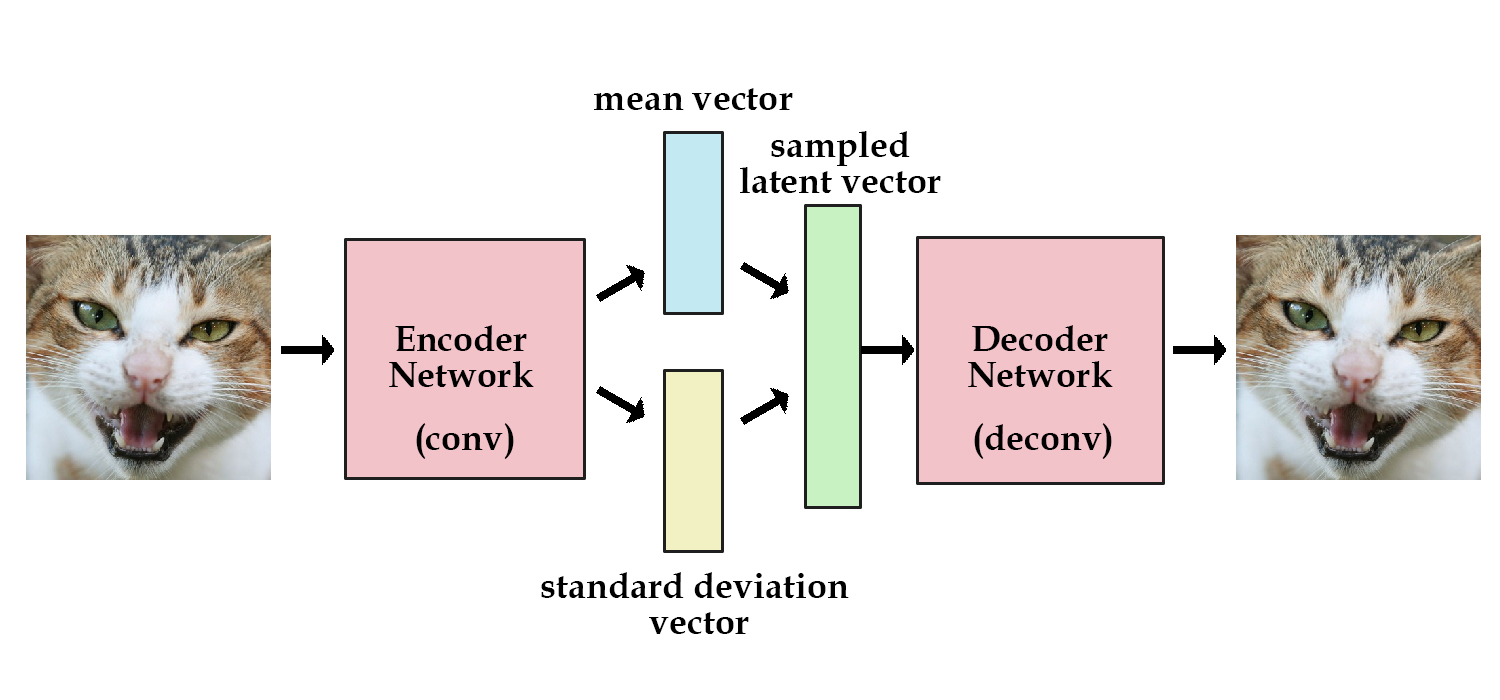
Structure of VAE.

EA is a special case of VAE, which simplified the calculation of the q(x,z).

Derive

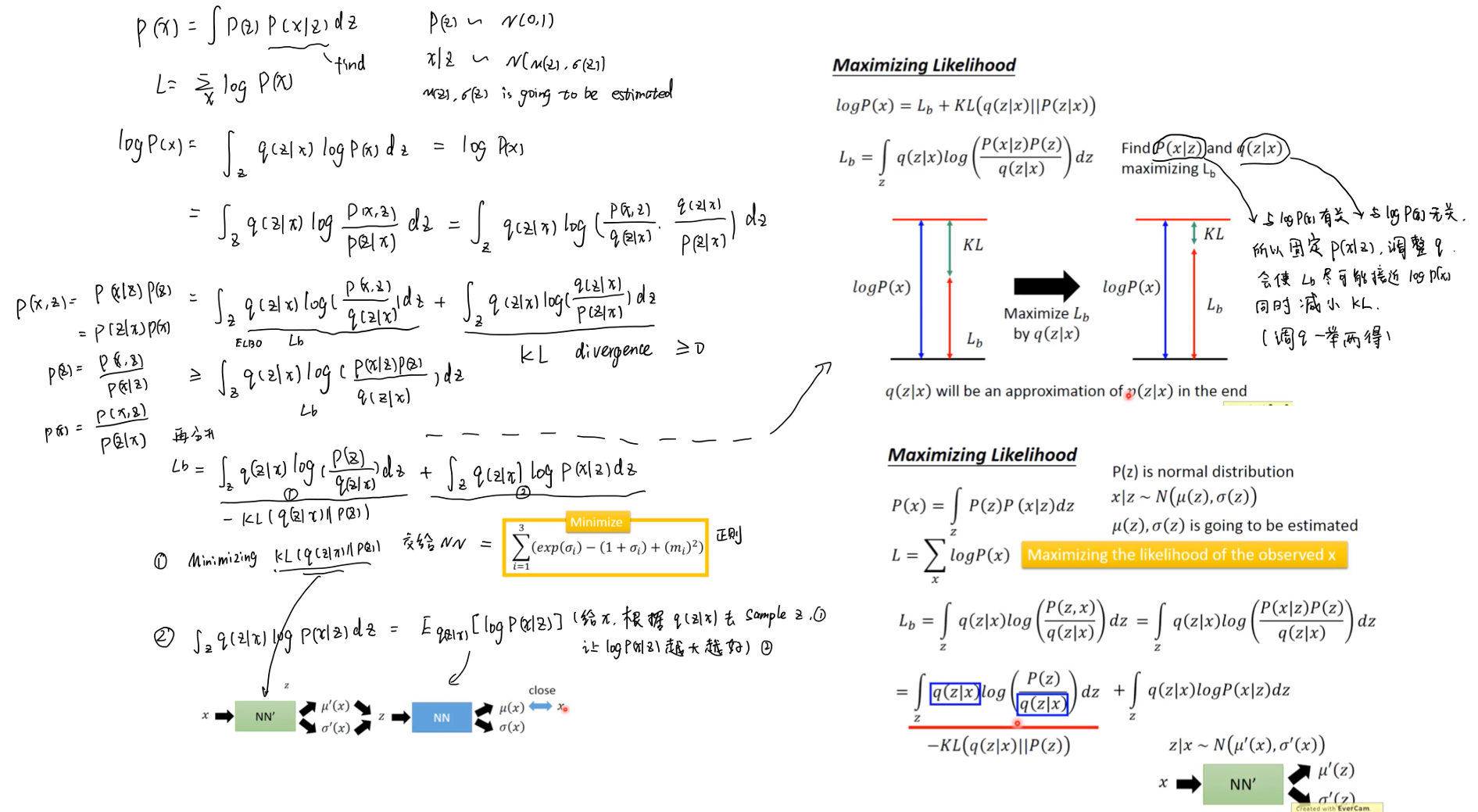
Derive of the Loss in VAE.

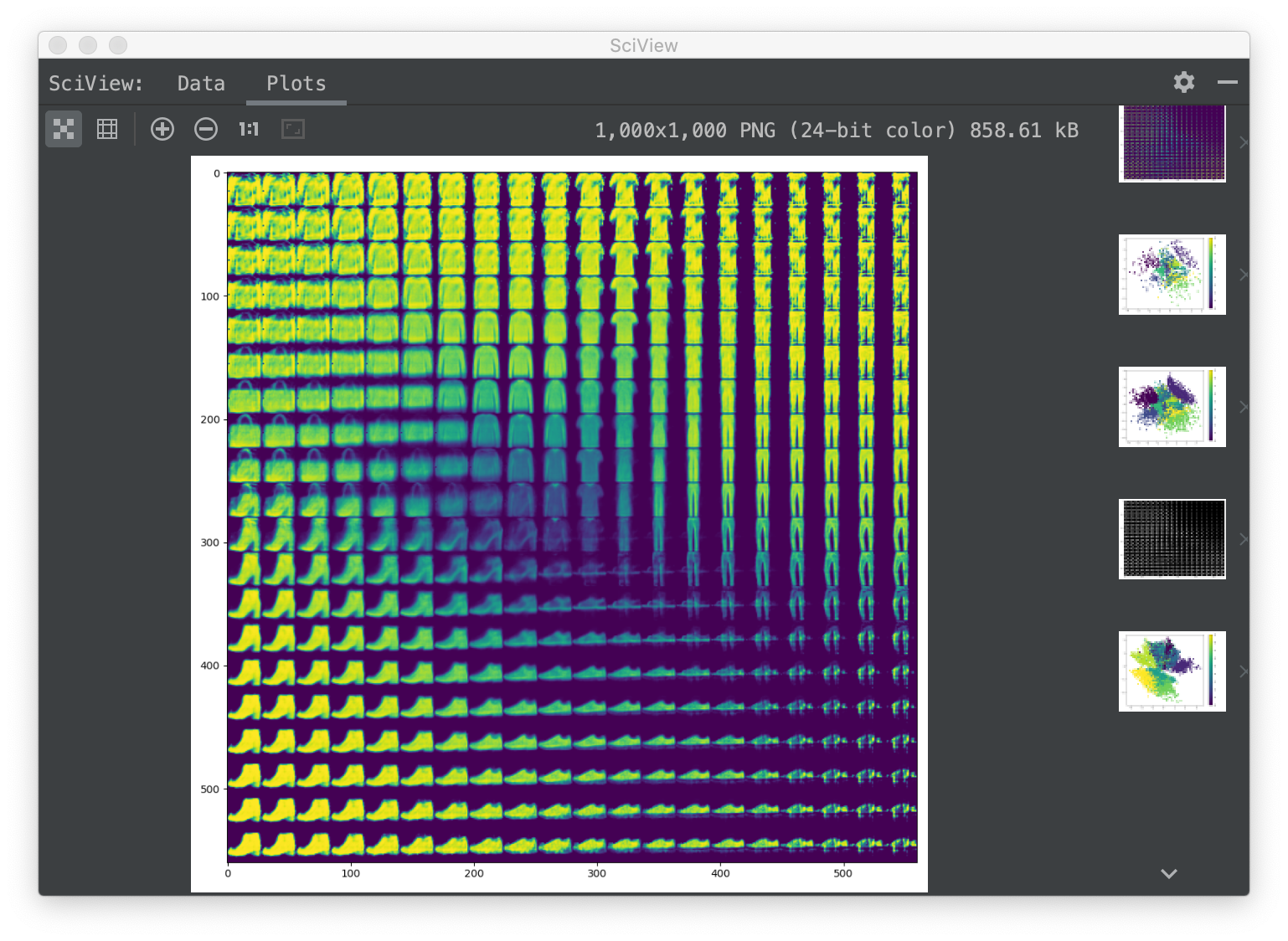
Result on MNIST

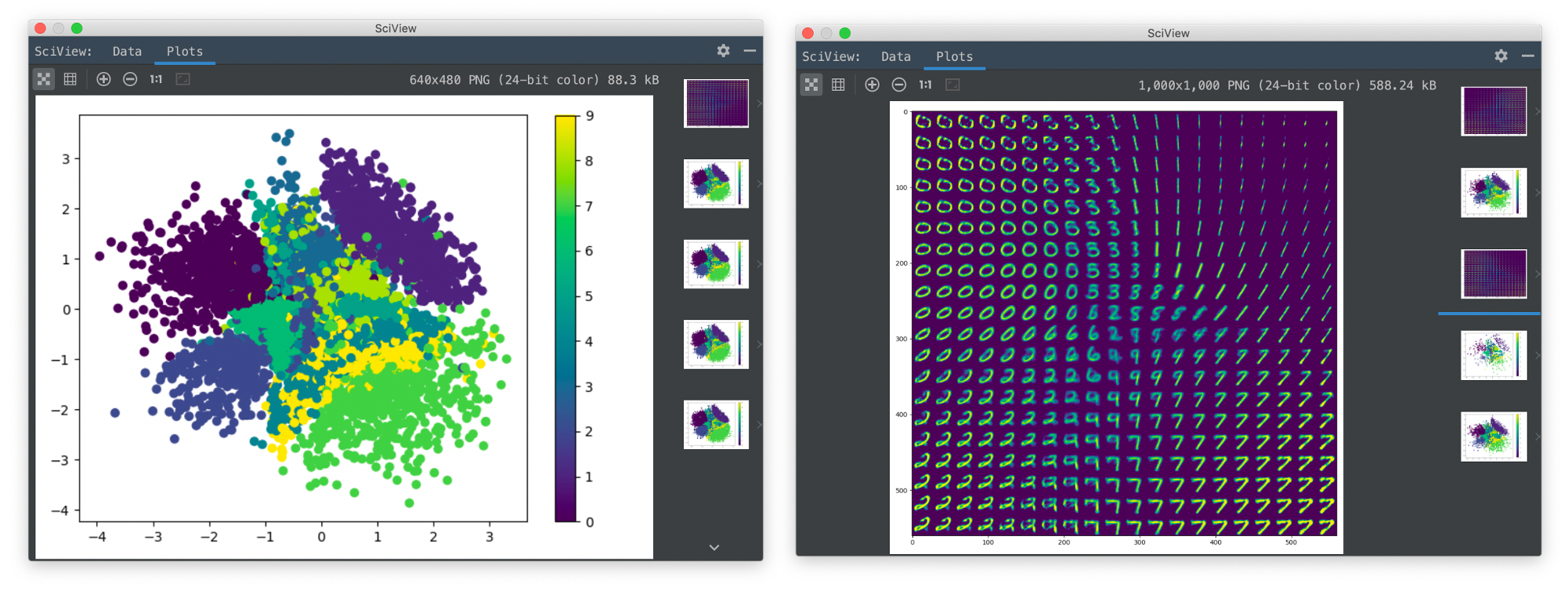
VAE on MNIST

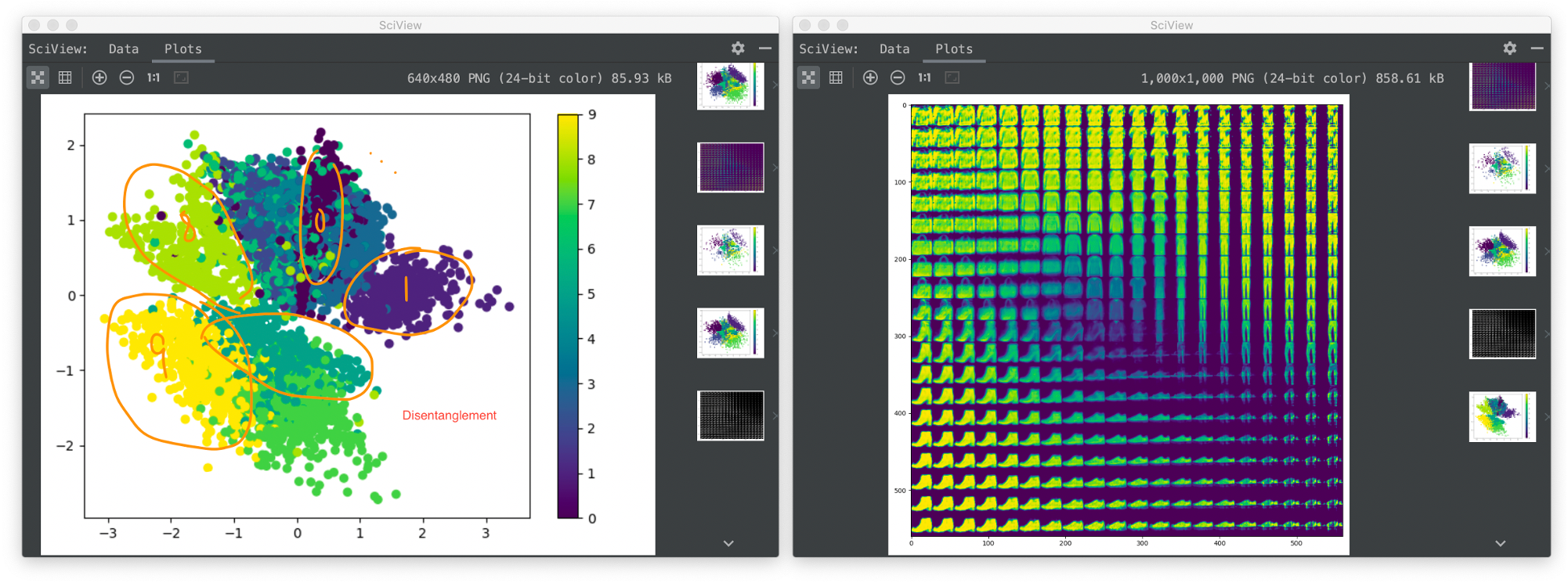
VAE on Fashion-MNIST

Issues

Resolution issue in VAE

I think VAEs is only imitating the input data instead of learning the feature like GAN. And MSE for loss will not be able to distinguish the good results from the bad ones.

Two results have the same loss

Contact

The above is the a brief description of EM and VAE. If you encounter unclear or controversial issues, feel free to contact Leslie Wong.