Evolution Algorithms: SaDE, DE

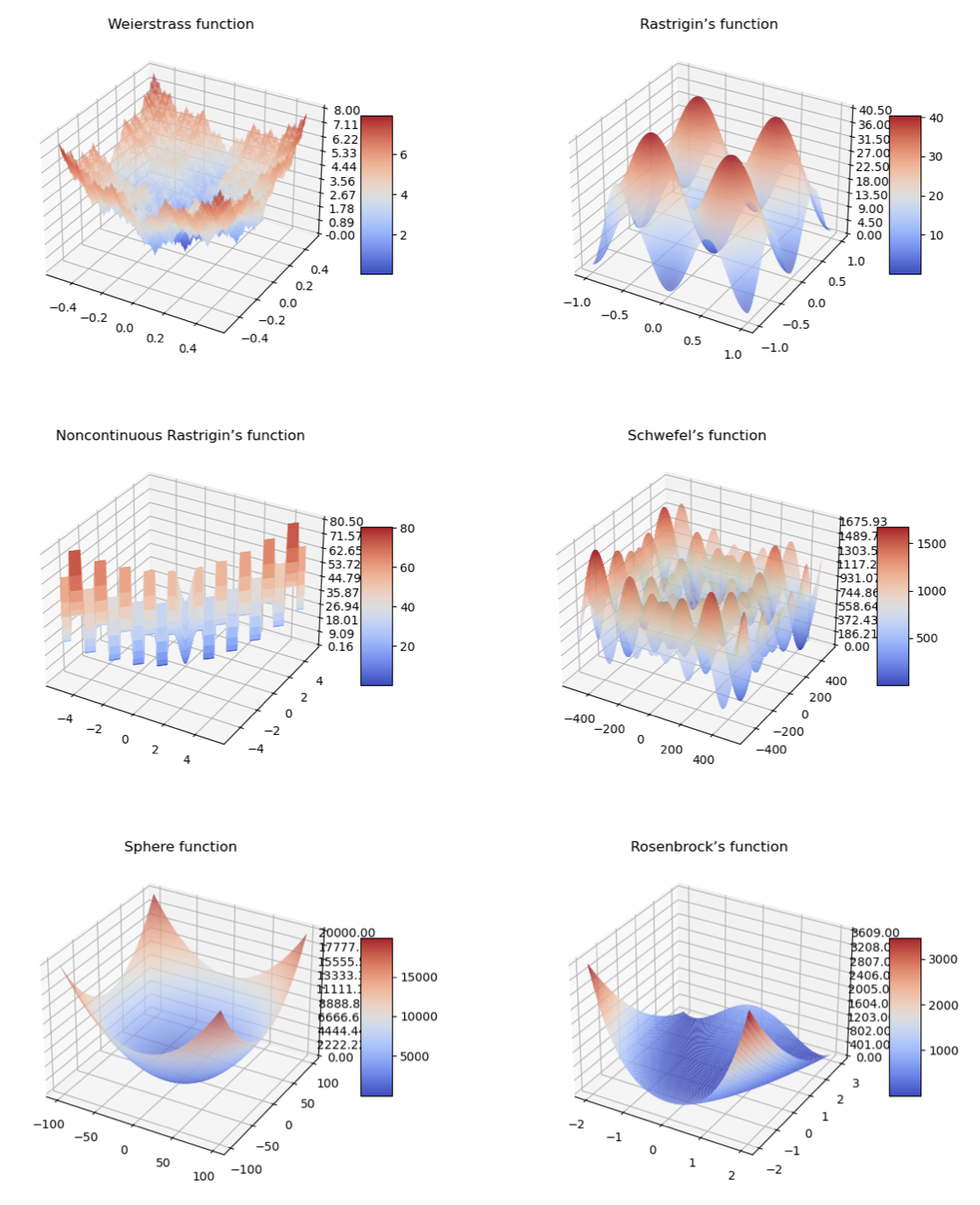
Testing Functions

What did I do

I compared several algorithms including: Differential Evolution, Self-Adaptive DE. I changed the different hyper parameters for each algorithm with the functions shown above.

Codes are available at: https://github.com/LeslieWongCV/EE6227_Wong/tree/main/DifferenceEvolution

Setup on which the code was tested

• python==3.6
• numpy==1.19.2

Test Functions

These are the test functions, data set are generated from them:

DE

DE is an old but powerful algorithm. As in definition: a stochastic population-based algorithm for continuous function optimization.

Features

1. DE is friendly for start-up programmers because it is easy to implement in mainstream programming languages from the basic level.
2. DE has very few control parameters (3 for standard DE), the influence of each parameter has been well studied.
3. Compared to some of the most competitive continues algorithms like CMA-ES, the spatial complexity of DE is very low.

Procedure

1. Initialize the population from range ∈ [Xi_Min, Xi_Max] randomly, where Xi_Min and Xi_max are the lower/upper bound of the particles and i denote the ith dimension of the decision number. Calculate the fitness score of the particles when finished initialization.

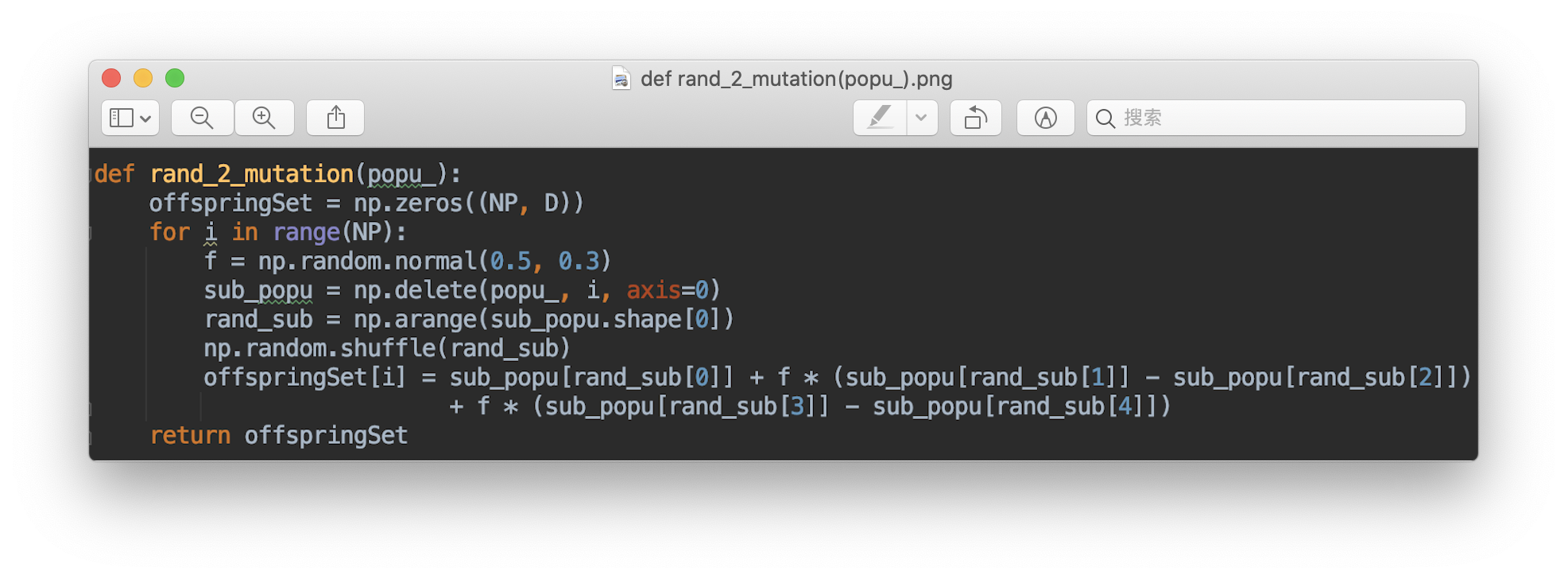
2. For each population member, select three other members randomly. Add the weighted difference of two with one left in the three members (mutation).
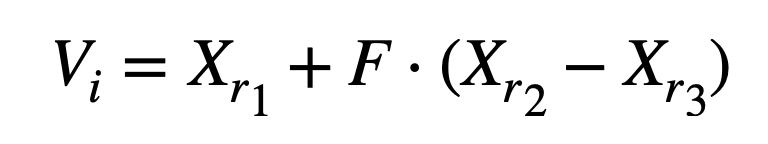
3. Generate a constant number Cr ∈ (0, 1) and for each decision variable, generate a random number randi, j ∈ [0, 1), generate the virtual children(U) as follows (crossover). In DE, each virtual child should at least has one dimension from parent.
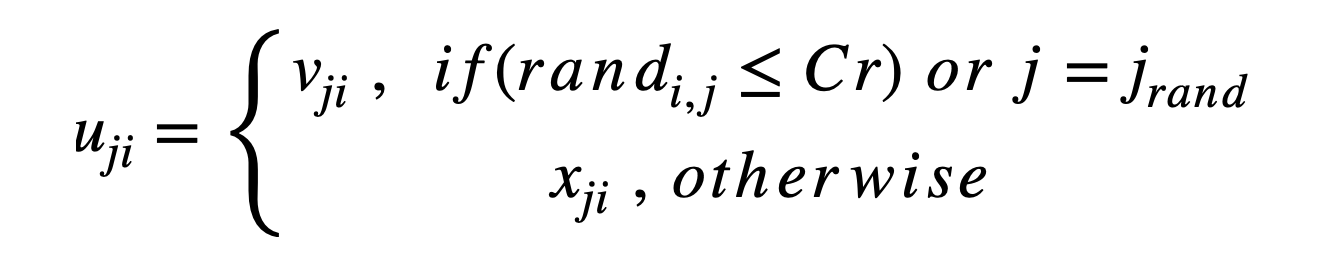
4. Compare the fitness score of parents and virtual children(U), individuals with higher score(in maximize problem) would remain.
5. Continue to process until the number of the iteration reaches a predetermined value; and break the loop after that.

Self-Adaptive DE (SaDE)

Self-Adaptive DE is an improved DE with both control parameter adaptation and strategy adaptation.

Strategy Adaptation

Instead of using single generation strategy, SaDE has more than one generation strategies:

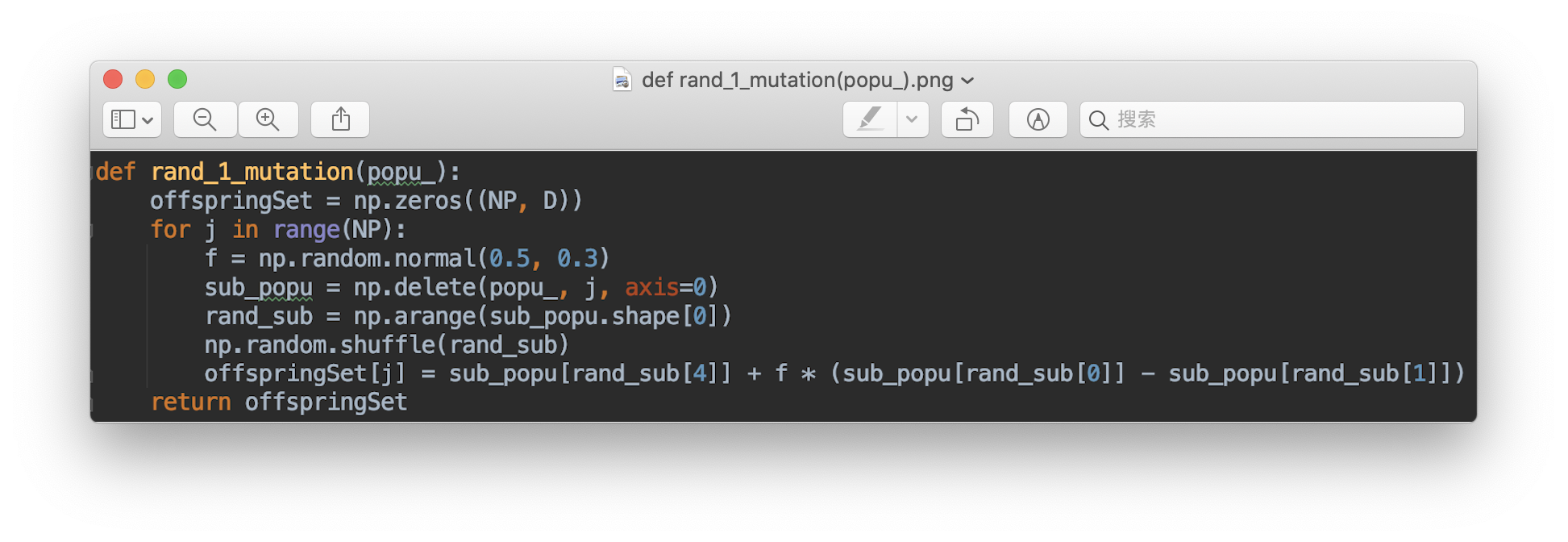
Strategies 1:

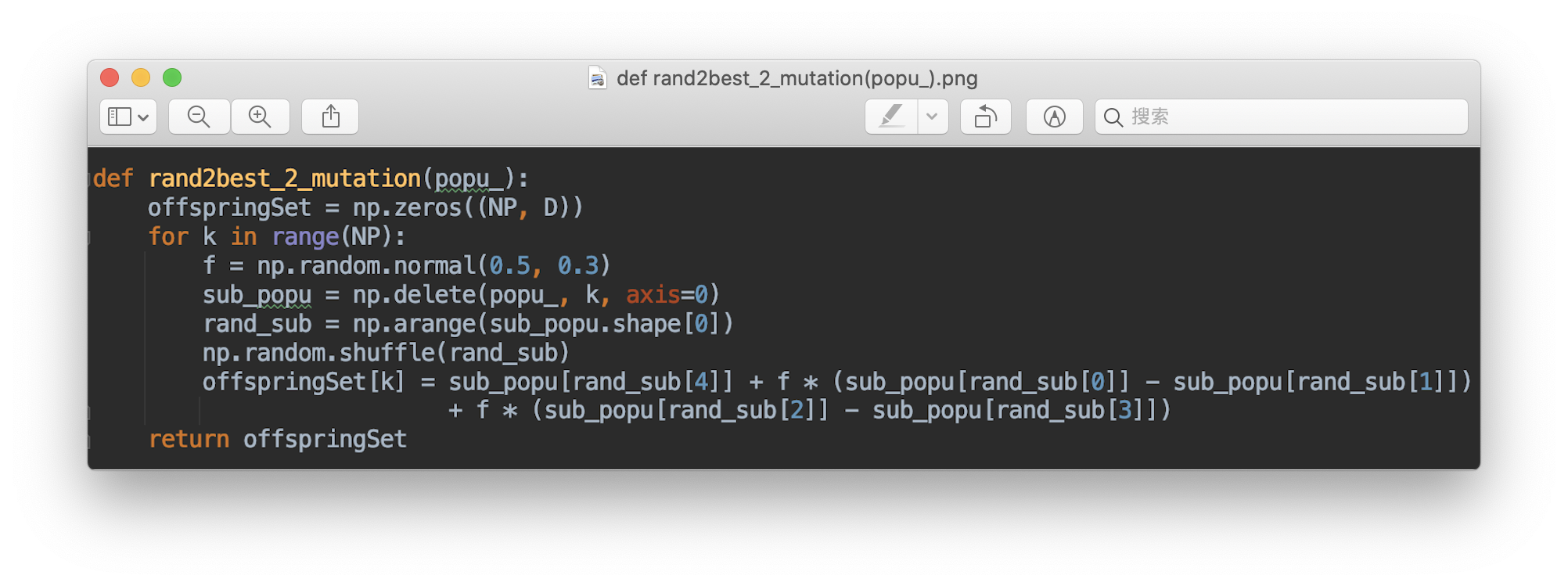
Strategies 2:

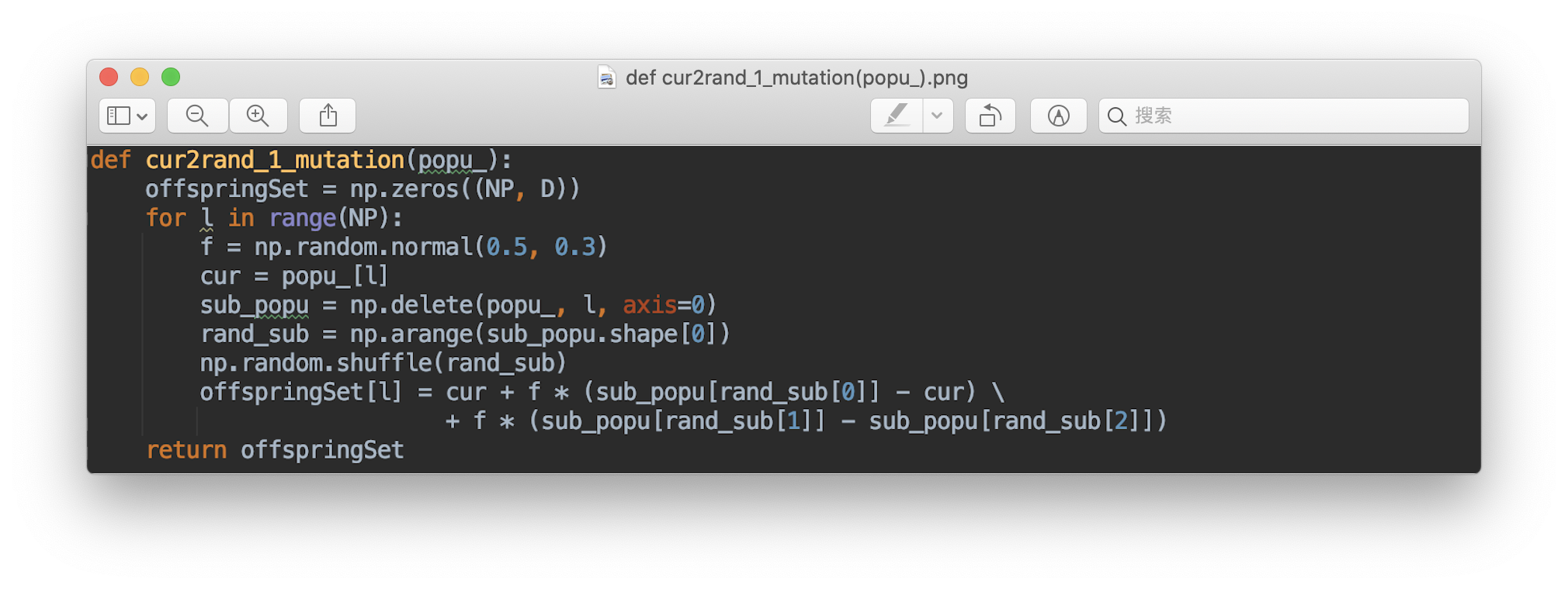
Strategies 3:

Strategies 4:

The general convention used for naming the various mutation strategies is DE/x/y/z, where DE stands for Differential Evolution, x represents a string denoting the vector to be perturbed, y is the number of difference vectors considered for perturbation of x, and z stands for the type of crossover being used (exp: exponential; bin: binomial) best: The best solution in the current population.

For each target vector in the current pool, one strategy is selected from the above according to its success rate in generating better offsprings.

Control Parameter Adaptation

The parameters in SaDE: NP - the number of individuals in the population Cr_m - the mean Cr of the offspring that replace the parent in the last Generation. Cr - the crossover rate Cr obey a normal distribution with mean value Cr_m, standard deviation at 0.1. F - a set of F values are randomly sampled from normal distribution N(0.5, 0.3).

SaDE gradually changes the range of Cr values for a given problem according to Cr_m, thus the algorithm would converge appropriately. In addition, having pre-runs to pick a better strategy make the algorithm sensitive to the data.

Contact

The above is the a brief description of DE, SaDE. If you encounter unclear or controversial issues, feel free to contact Leslie Wong.